2.1 几个典型的随机事件
管理系统模拟涉及的问题大量的都属于随机事件,因此首先从随机事件的模拟开始,先学习了解随机时间模拟的方法和特点,由易到难循序渐进是很有必要的。
2.1.1 掷骰子实验
抛掷一枚骰子可能的结果是6个面出现6个不同的点,究竟会出现哪个点,显然属于随机事件。相关的问题是:(1)抛掷一枚骰子,观察朝上一面的点数,出现6个不同点的可能性(概率)各是多少?(2)如果同时掷出3枚骰子,又会出现什么结果?每个结果出现的概率是多少?
先分析问题(1),从理论上我们不难知道,如果骰子的6个面都是均匀的,没有任何一个面沾有铅或其它重物,那么每个面出现的机会应该是均等的,即各有1/6的概率。毫无疑问,这一点可以通过模拟来证明。
下面运用Excel模拟掷骰子的实验。模拟过程是:
(1)在A1单元格输入“=INT(RAND() 6)+1”或者“=TRUNC(RAND() 6)+1”,可产生一个大于或等于1,小于或等于6的自然数。这一步也可以通过函数“=RANDBETWEEN(1,6)”完成。
(2)将单元格A1复制拖放到A2直至A1000。
(3)运用FREQUENCY函数分别统计A1到A1000中数字1、2、3、4、5、6出现的个数,将结果分别存入C1~C6中,也可以在C1单元格中输入“=COUNTIF(A1:A10000,1)”,在C2格输入“=COUNTIF(A1:A10000,2)”等等。
(4)分别计算数字1、2、3、4、5、6出现的频率。
容易看出,结果跟理论分析是一样的。
对案例1中的问题(2)进行模拟,同样需要先进行理论分析。
同时掷出3个骰子的结果如表1所示。
表1 同时掷出3个骰子的结果
|
结果 |
频数 |
概率% |
ABC组合 |
|
3 |
1 |
0.463 |
111 |
|
4 |
3 |
1.39 |
211,112,121 |
|
5 |
6 |
2.78 |
311,212,221,122,131,113 |
|
6 |
10 |
4.63 |
411,313,331,222,213,231,123,132,141,114 |
|
7 |
15 |
6.94 |
511,421,412,322,313,331,223,232,214,241,133,124,142,115,151 |
|
8 |
21 |
9.72 |
611,512,521,422,413,431,323,332,314,341,233,224,242,215,251,134,143,125,152,116,161 |
|
9 |
25 |
11.57 |
612,621,522,513,531,423,432,414,441,333,324,342,315,351,234,243,225,252,216,261,144,135,153,126,162 |
|
10 |
27 |
12.5 |
622,613,631,523,532,514,541,433,424,442,415,451,334,343,325,352,316,361,244,235,253,226,262,145,154,136,163 |
|
11 |
27 |
12.5 |
155,146,164,245,254,236,263,344,335,353,326,362,434,443,425,452,416,461,533,524,542,515,551,623,632,614,641 |
|
12 |
25 |
11.57 |
165,156,255,246,264,345,354,336,363,444,435,453,426,462,534,543,525,552,516,561,633,624,642,615,651 |
|
13 |
21 |
9.72 |
166,265,256,355,346,364,454,445,436,463,544,535,553,526,562,634,643,625,652,616,661 |
|
14 |
15 |
6.95 |
266,356,365,455,446,464,545,554,536,563,644,635,653,626,662 |
|
15 |
10 |
4.63 |
366,456,465,555,546,564,645,654,636,663 |
|
16 |
6 |
2.78 |
466,565,556,655,646,664 |
|
17 |
3 |
1.39 |
566,656,665 |
|
18 |
1 |
0.463 |
666 |
|
合计 |
216 |
100 |
—————————— |
这个问题有趣的是对掷3枚骰子所得结果组合的罗列。
请仔细观察表1的最后一列。“结果”一列从3~8,“ABC组合”中的第一个组合打头的数字从1~6,每一种结果中该组合都只有一个,接下来分别是1~5打头的,相应的组合数都只有2个,再下来分别是1~4打头的,相应的组合数都只有3个,再下来分别是1~3打头的,相应的组合数都只有4个,如此等等。
再从表1的倒数第二行往上看。“结果”一列从18降到13,“ABC组合”中的第一个组合打头的数字从6降到1,每一种结果中该组合都只有1个,接下来分别是6、5、4、3、2打头的,相应的组合数都只有2个,再下来分别是6、5、4、3打头的,相应的组合数都只有3个,再下来分别是6、5、4打头的,相应的组合数都只有4个,如此等等。
掷出3枚骰子的模拟过程与掷出1枚骰子的模拟过程差不多,只是需要同时生成3组随机数而已。
2.1.2 随机抽样——抓阄
学生会给某班(30个人)5张电影票,大家都想要,于是班长就在30张纸条中的5张上都做了记号,然后让每个人随机抽一张,凡抽到有记号的纸条就给他一张电影票。求第k个(1≤k≤30)人抽到有记号纸条的概率。
或许有人认为,先摸,模到的概率将会大些。是否真是这样?如果先摸到有记号的纸条概率大些,此方法就不会长久而广泛地被采用列今天。在这里,每个人摸到有记号的概率都是1/6,不管是先摸还是后摸,也不管是采用有放回还是无放回抽样,都一样。当然,不排斥抓阄抓到一半或大半时做了记号的被抽完的情况,但同样也会出现抓阄抓到了一半或大半时做了记号的一个都没有抽到。为了避免这些极端情况的出现,有人认为抓阄时最好采用有放回抽样。实际上,有放回和无放回都是一样的。
抓阄问题可归纳为下面更一般的摸球问题。
一个袋中有n个白球m个黑球,现不放回地从袋中摸球,求第k次模到黑球的概率,k=1,2,…,n+m。
用数学方法可以证明,不管是先摸还是后摸,摸到黑球的概率都是一样的。同样也可以证明,不管是有放回地摸还是无放回地摸,概率也都是一样的。
如果设Ak=“第k次摸到黑球”,k=1,2,…,n+m,运用排列组合方法不难证明:对任意正整数k(1≤k≤n+m),不管是先摸还是后摸,也不管是有放回还是无放回,均有
![]()
证明过程此处省略。
与此问题相关的一个问题是,一个袋中有n个球,其中有m个是黑色的。现从中摸k个球(有放回或无放回均可)。已知摸出的k个球中有r个是黑的,求第j(j=1,2,…,k)次摸到黑球的概率。在这里,不论是有放回的还是无放回的,结论都是一样的,概率都是r/k,且一定有r/k≈m/n。
现在我们通过模拟来证明这一原理。
先做有放回抽样。
有放回抽样就是说每次抽样的总体是不变的。现假定总体n=100,其中黑球数m=10,为方便演示,我们假定这100个球都编了号,其中的黑球是1~10号。这种模拟通过两步即可实现。
第一步,使用函数“=INT(1+100*RAND())”或“=RANDBETWEEN(1,100)”生成一个1~100之间的随机数;
第二步,使用函数“IF(B11<11,1,0)”(假定第一个函数在B11单元格)统计小于等于10的随机数;
最后,使用函数“=COUNTIF(L11:L1510,1)”(假定模拟了1500次)汇总小于等于10的随机数,并计算概率。不难发现概率稳定在10%左右。
这种实验与实际情况是一致的。因为抽样是由随机数的发生机制确定的,由于随机数生成的随机性,因而在100次抽样中抽到的黑球数(小于10的随机数)可能大于10,也可能小于10,这也就是平均概率在10%左右波动的原因。而实际的情况是,由于抽样是有放回的,因此在100次抽样中,摸到黑球的总数可能大于10,也可能小于10。这一点是不难理解的。
再做无放回抽样。无放回抽样总体会发生变化,仍假定总体n=100,其中黑球数m=10,同时也需要对100个球编上号,其中的黑球是1~10号。这里不同于有放回抽样的是,当抽样100次后,总体就被抽完了,因此为了通过多次模拟获得稳定的概率,需要由一个新的总体重新开始。模拟的过程是:
第一步,先在D10单元格输入100,然后使用函数“=IF(D10=0,D10+99,D10-1)”确定总球数,每试验一次总球数减少一个,当总球数为0时,加上99重新开始。
第二步,使用函数“=INT(1+D11*RAND())”在E11单元格生成1~100的随机变量。试验的第一轮,10号以下为黑球,其余为白球。
第三步,先在F10单元格输10,然后使用函数“= IF (F10=0, IF(D10=0, F10+10,F10), IF(E11>F10,F10,F10-1))”确定黑球的数目。
第二步和第三步有一个隐含的假定,即如果摸到的是白球,不管这个白球是多少号,就用这个白球换出白球的最后一个号;如果摸到的是黑球,同样不管这个黑球是多少号,就用这个黑球换出黑球的最后一个号,同时白球的编号也依次向前移动。也就是说,每次抽样以后,都需要对全部对象重新编号。
第四步,使用函数“=IF(E11<F10+1,1,0)”反映摸出的是否黑球。
最后,使用函数“=COUNTIF(G11:G1510,1)”统计摸出的黑球数目,并计算概率。不难发现,概率稳定在10%上。
为什么概率会稳定在10%上?这不难理解,因为抽样是不放回的,因此在100次抽样中,抽到的黑球数只能是10,不会大于10,也不会小于10。这一点很容易理解。
2.1.3 圆纸板问题
设想地上铺有80×80cm的地砖。现在拿一个硬纸板制作的圆形纸板,随机地向地面上抛掷,假定纸板的直径为20cm,问题是:(1)纸板与地砖的任一缝隙相交的概率是多少?(2)纸板与四块地砖构成的十字线相交的概率又是多少?
先进行理论分析。
对该问题进行理论分析,容易理解,对于问题一,只有当圆纸板的中心距离地砖的缝隙小于等于10cm时,纸板才可以与地砖的缝隙相交。假定用x和y分别表示圆纸板圆心的坐标,则可知圆纸板相交的条件为:
0≤x≤10或70≤x≤80,0≤y≤10或70≤y≤80
放在如图1所示的示图上说,即如果x和y的数值落在图中的小矩形内,就不相交,两个变量的数值只有落在图中的灰色区域内才相交。
也就是说,圆纸板与地砖任一缝隙相交的概率为:
![]()
对于问题二,显然只有当纸板的中心落在如图1所示的大正方形的四个角10×10的范围内才是可能的,因此相交的概率为:
![]()
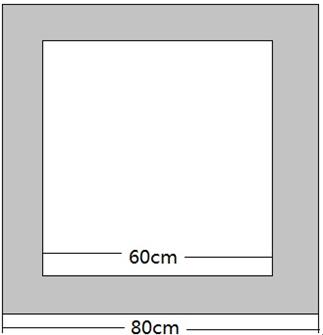
图1
下面用Excel来进行模拟。
对于问题一的模拟有两步就可以解决问题。
第一步,先用公式“=80*RAND()”生成两个随机数,分别表示圆纸板距离地砖缝隙的距离,也就是x和y的坐标值。
第二步,利用公式“=IF(S11<10,1,IF(S11>70,1,IF(T11<10,1,IF(T11>70,1,0))))”记录相交的次数,即相交记为1,不相交记为0。
这一步也可以通过函数“=IF(OR(S11<10,S11>70,T11<10,T11>70),1,0)”实现。在这里,函数“OR()”使用的格式是OR(logical1,logical2,…),其中的条件只要满足一个即可;相应地,如果有多个条件需要同时满足,可使用“AND()”函数,使用的格式与OR函数相同。在对第二个问题模拟时就需要用到“AND()”函数,
这两步完成后将全部3列一起拖放1500行,即模拟1500次。
最后,在划出的统计输出区利用公式“=SUM(S11:S1510)”统计相交的次数(这里第二步的函数在s列),利用公式“=(S4/1500)*100”计算概率值。
重复按“Delete”键(或F9键)就得到多个频率,可发现它在43%~45%附近摆动。
对于问题二,第一步与问题一相同。第二步,利用函数“=IF(OR(AND (S11<10,T11<10), AND(S11<10,T11>70),AND(S11>70,T11<10),AND(S11>70,T11>70)),1,0)”记录相交的次数,最后使用SUM函数统计相交的总次数,计算概率,使用F9键重复试验,可发现概率稳定在6%~7%之间。
上述几个问题的模拟表参见光盘数据文件“模拟数据2”中的“随机事件”一页。
